Imagine a world where you can prove the truth of a statement without revealing any details about the statement itself. It sounds paradoxical, doesn’t it? How can one demonstrate knowledge of a secret without disclosing that secret? In this article, we delve deep into the fascinating world of zero knowledge proofs, a mathematical technique that accomplishes this seemingly impossible feat. We will explore the concept, its practical applications, and the profound implications it has, especially in the fields of computer science and cryptography.

The Gummy Bears Game

To grasp the essence of zero knowledge proofs, we will start with a small game. Imagine we have a jar of gummy bears, and I pick two gummy bears from it. I claim that these gummy bears are of different colors but refuse to show or disclose their colors to you. How can I convince you that my claim is true without revealing the actual colors of the gummy bears?

Here’s how the game unfolds: First, I will place the gummy bears that I’ve picked, each under one cup. Then, I will close my eyes and you have the option to either switch the cups or leave them as they are. After that, I take a look under each cup and correctly reveal to you whether you’ve switched the cups or not. Sound pretty intuitive right? Had the gummy bears I chose where of the same color, I wouldn’t know whether the cups were switched or not.

Aha! “You’ve just gotten lucky”, you tell me. So we repeat the game over and over again, making it increasingly improbable that with every correct answer I am merely guessing. In fact, after several rounds, the chances of guessing correctly every time become so minuscule that it’s practically impossible.

To put this more into perspective, the probability of guessing correctly in each round is 50-50 (or 1 in 2). So, after two rounds, the probability of guessing correctly twice in a row is 1 in 4. We can keep repeating this process as many times as needed to make it highly improbable that the correct guesses are due to luck alone. If we want the chances of me lying to be less than 1%, we only need to repeat the process a total of seven times. The probability of me guessing correctly every time without knowing the gummy bears’ colors becomes infinitesimally small, approaching zero.

While this doesn’t provide a strict mathematical proof, it demonstrates the concept of zero knowledge: you can convince someone that you know a true secret without revealing any details about that secret. This scenario aligns with the principles of a ZK proof.

The idea of not having a “strict proof” is a very important aspect of zero knowledge proofs. It poses questions like: “At what point does the game end?” or “What’s the lowest probability that show the prover is not just guessing but actually has the required knowledge?”. Of course, the answer to that depends on each game and the rules agreed upon by the players. For our example, we could both agree that you would trust me after guessing the first twenty consecutive rounds correctly.

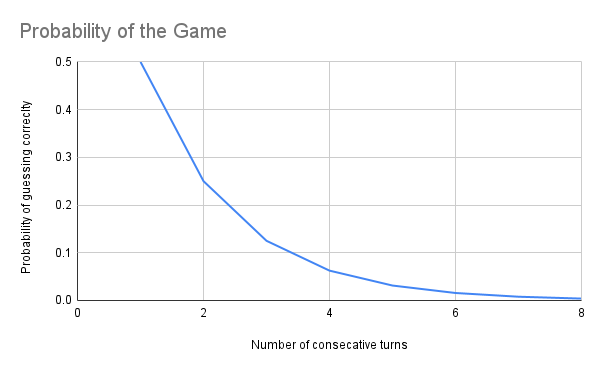
If anything, the gummy bears game we played is rather simple. Had I picked 10 gummy bears with distinct colors, the probability of me guessing correctly becomes less than 1% in just the third turn! Of course, we could make the game even more complex by adding different conditions like having 3 gummy bears out of 10 to be of the same color, or adding different gummy animals and changing the rules of our game accordingly; you get the idea. We are basically free to do whatever we want as long as we follow the 3 rules of zero knowledge proof.

The Three Pillars of Zero Knowledge Proofs(ZK proof)

For a system to qualify as a zero knowledge proof, it must satisfy three fundamental conditions: completeness, soundness, and zero knowledge.

1. Completeness

Completeness ensures that when the prover genuinely possesses the secret, and both parties follow the protocol correctly, the verifier will agree that the prover indeed knows the secret. In our gummy bears game, this means that when I truly know the gummy bears’ colors and both me and you follow the rules, you will be convinced that I posses the secret.

2. Soundness

Soundness guarantees that it is impossible for the prover to prove anything false using the zero knowledge proof system. In our game, this means that in order for it to finish, we must be able to reach the goal we’ve set for it, which would only be possible if my claim of having two distinctly colored gummy bears is true.

3. Zero Knowledge

Zero knowledge is, as the name suggests, the most intriguing and important aspect of zero knowledge proofs. It ensures that the verifier gains no additional knowledge beyond the fact that the prover knows the secret. In our example, you do not learn the actual colors of the gummy bears I’ve picked, only that they are different. An eavesdropper, cannot discern whether the proof is genuine or fabricated, they would simply hear “switched” or “not switched”.

Why Zero Knowledge Proofs?

Zero-knowledge proofs (ZKPs) are important for several reasons:

1. Privacy and Security: ZKPs allow for the verification of information without revealing the underlying data, providing a high level of security and privacy. This is particularly useful in situations where sensitive information needs to be kept confidential, such as in financial transactions or personal identification. ZKPs ensure that only the necessary information is disclosed, while keeping the rest private.
2. Compliance: ZKPs can help organizations comply with various regulations, such as data privacy laws. They can also be used to provide secure and private identity verification for compliance with know-your-customer (KYC) and anti-money laundering (AML) regulations. ZKPs enable organizations to prove compliance without revealing sensitive data.
3. Data Sharing: ZKPs can facilitate secure data sharing between parties. With ZKPs, one party can prove the validity of certain data or claims to another party without revealing the actual data. This allows for secure collaboration and sharing of information while maintaining privacy.
4. Blockchain Technology: ZKPs have significant applications in blockchain technology. They can be used to enhance privacy and confidentiality in blockchain transactions, ensuring that sensitive information remains hidden while still providing proof of the transaction’s validity. ZKPs can also enable secure and private smart contracts, where parties can interact without revealing their private inputs.

Overall, zero-knowledge proofs provide a powerful tool for ensuring privacy, security, and compliance in various domains, including finance, healthcare, identity verification, and blockchain technology. They allow for the verification of information without revealing unnecessary details, enabling secure and private interactions between parties.

Types of Zero Knowledge Proofs

There are several types of zero-knowledge proofs, each with its own characteristics and areas of application. Here are three prominent types of zero-knowledge proofs:

ZK-SNARKs (Zero-Knowledge Succinct Non-Interactive Argument of Knowledge):

• ZK-SNARKs are highly efficient and compact zero-knowledge proofs that can prove the validity of a statement without revealing any additional information.
• They are non-interactive, meaning the proof can be generated by a prover and verified by a verifier without the need for back-and-forth communication.
• ZK-SNARKs are widely used in privacy-focused blockchain platforms like Zcash to provide transaction confidentiality while ensuring the integrity of the blockchain.

ZK-STARKs (Zero-Knowledge Scalable Transparent Argument of Knowledge):

• Unlike ZK-SNARKs, ZK-STARKs are transparent zero-knowledge proofs that do not rely on trusted setups. They offer post-quantum security and are highly scalable.
• ZK-STARKs are suitable for complex computations, making them valuable for applications like verifying computations on large datasets, decentralized exchanges, and digital asset management.

Bulletproofs:

• Bulletproofs are a type of zero-knowledge proof designed to provide efficient and confidential range proofs for confidential transactions.
• They offer a compact representation, reducing the size of the proofs compared to previous approaches, while ensuring privacy and verification of range constraints.
• Bulletproofs are commonly used in privacy-focused cryptocurrencies like Monero to enhance transaction privacy.

These are just a few examples of zero-knowledge proofs, each serving different purposes and offering unique benefits. Other types, such as ZK-Rollups and ZK-Plonk, are also being developed and utilized for specific use cases. The choice of zero-knowledge proof depends on the requirements of the system or application and the specific trade-offs between security, efficiency, and scalability.

What are the Disadvantages of Zero Knowledge Proof?

While zero-knowledge proofs offer significant advantages in terms of privacy and security, they do come with certain disadvantages. Here are a few key disadvantages of zero-knowledge proofs:

• Computational Complexity: Zero-knowledge proofs can be computationally expensive, requiring significant computational resources and time to generate and verify proofs. This complexity can limit their scalability in certain applications, especially those with strict real-time requirements.
• Technical Expertise Requirements: Implementing zero-knowledge proofs requires expertise in cryptography and advanced mathematical concepts. Developing and correctly implementing these proofs can be challenging and may require specialized knowledge, making it less accessible for developers without a strong background in these areas.
• Trusted Setup: Some zero-knowledge proof systems, such as ZK-SNARKs, rely on a trusted setup phase. This setup process can introduce a level of trust in the entities responsible for generating the initial parameters, potentially undermining the trustless nature of blockchain systems.
• Assumption Reliance: The security of zero-knowledge proofs often relies on the assumption that certain cryptographic functions are secure and that specific mathematical problems are difficult to solve. If these assumptions are compromised or found to be insecure, it could undermine the overall security of the zero-knowledge proof system.
• Performance Overhead: Verifying zero-knowledge proofs can introduce additional computational overhead compared to traditional authentication or validation methods. This overhead may impact system performance, particularly in high-throughput scenarios.

It is important to carefully consider these disadvantages in the context of the specific use case and requirements of the system. While zero-knowledge proofs offer notable benefits, understanding and mitigating these disadvantages are crucial for effective and secure implementation.

Real-World Applications

Zero knowledge proofs have evolved from a theoretical concept to a practical tool with significant real-world applications. One of the most notable areas where zero knowledge proofs are making a difference is in the realm of cryptocurrency.

In the early days of cryptocurrency, trust and privacy were at odds. The invention of Bitcoin introduced the concept of the blockchain, a public ledger that records all transactions. While the blockchain ensures transparency and trust in the system, it compromises user privacy. For example, anyone can see if a user paid for sensitive services like medical treatment. Zero knowledge proofs have changed this equation.

Today, certain cryptocurrencies employ zero knowledge proof algorithms to verify the blockchain without revealing transaction details. This means that while the blockchain remains publicly accessible, the contents of individual transactions remain hidden, preserving user privacy.

You can read more about zero knowledge proofs and their remarkable uses in blockchain in this fantastic article by the Ethereum Foundation.

Of course, the power of zero knowledge proofs extends beyond cryptocurrencies. It applies to any mathematical proposition that has a valid proof. A mathematical proposition is a statement that is either true or false, such as the Pythagorean theorem.

A quick and easy example of a mathematical zero knowledge proof is by imagining someone who claims to have discovered a secret prime number but doesn’t want to reveal the number itself. They want to prove their claim without giving away the number.

In a zero knowledge proof scenario, the person claims that their secret number is prime. The verifier then challenges them to demonstrate divisibility tests. For example, the prover may have a calculator where the number is saved, and the verifier can ask them about the remainders of division operations to the prime number with a number of their choice except the number one. The only way the remainder of any division operation is different from zero is by guessing the number itself which no longer makes it a “secret number” thus making the challenge invalid. The verifier, after enough divisions, becomes convinced of the primality of the secret number without ever learning the number, fulfilling the zero knowledge proof requirements.

Conclusion

Zero knowledge proofs have revolutionized our understanding of proof, transforming it from a static concept into an interactive and cryptographically secure game. These proofs have found applications in cryptocurrency, mathematics, and beyond; offering a unique blend of trust, privacy, and mathematical elegance. As we continue to unlock the secrets of zero knowledge proofs, we open new doors to innovation and secure communication in the digital age.

1. What is a zero knowledge proof?

A zero knowledge proof is a cryptographic technique that allows one party to prove the truth of a statement to another party without revealing any additional information beyond the statement’s validity.

2. How does a zero knowledge proof work? 

Zero knowledge proofs utilize interactive protocols, cryptographic operations, and mathematical techniques to enable a prover to convince a verifier of a statement’s truth without disclosing sensitive information.

3. Are zero knowledge proofs secure?

 Yes, zero knowledge proofs are designed to be secure by utilizing cryptographic primitives and mathematical concepts. However, the security also depends on the correctness of the implementation and the underlying cryptographic assumptions.

4. What are the limitations of zero knowledge proofs? 

Zero knowledge proofs can be computationally intensive, requiring significant computational resources. Implementing them correctly can also be challenging and may require specialized knowledge in cryptography.

5. What are some real-world examples of zero knowledge proofs?

 Zero knowledge proofs have applications in privacy-enhanced authentication, confidential transactions, secure data sharing, and decentralized identity systems, among others.

6. Are there different types of zero knowledge proofs? 

Yes, there are various types of zero knowledge proofs, including zk-SNARKs, zk-STARKs, and bulletproofs, each with its own characteristics and use cases.

7. How will zero knowledge proofs evolve in the future?

 Ongoing research and development aim to enhance the efficiency, scalability, and usability of zero knowledge proofs, making them more accessible and practical for a wide range of applications